O(V + E) Algorithm - Breadth-First Search

上一篇介绍了哈希表，这一篇我们来讨论关于图（graph）的内容及一个非常实用的算法-- 广度优先搜索（Breadth First Search, aka BFS）。

一个图由节点（node）和边（edge）组成，而且如果节点A可以直接到达的节点B，那么称B是A的neighbor，如：

  ---      ---      ---
 | A | -> | B | -> | C |
  ---      ---      ---

B是A的neighbor，C是B的neighbor，但是C不是A的neighbor。

上面的图的边是带箭头的，我们称这样的图为有向图（directed graph），边不带箭头的为无向图（indrected graph）。如果是无向图的话，只要两个节点有边连接，那么这两个节点便互为neighbor。

如果给图的边加上权重（weight），那么图就变成了weighted graph，反之，就是unweighted graph。

在了解了图的基础知识之后，我们来介绍广度优先搜索（Breadth First Search, aka BFS），这个算法可以用来对有向无权重图（directed unweighted graph）做两件事情：

判断一个节点是否可以到达另一个节点
如果一个节点可以到达另一个节点，那么求两者之间的最短路径

第一件事我是已经理解了的，至于第二件事，更多的会使用Dijkstra's Algorithm去求解。虽然Dijkstra's Algorithm 一般是用来求解有向加权图的最短路径，但是无权图也可以看作各边权重相等的加权图，因此也可以用Dijkstra's Algorithm 来求解，这里就不做介绍了，等下一篇介绍Dijkstra's Algorithm的时候再细讲。

好，现在我们来描述BFS的算法，假设我们想找一个有向无权重图中节点A是否可以到达节点B，我们可以这样做：

1. 先把节点A的所有neighbors加入对列
2. 从对列中取出一个节点，先判断它是否已经被检查过。如果已经被检查过，
   那么就跳过它。如果没有被检查过，则判断它是否为节点B。如果是，则
   返回True；反之则将该节点的所有neighbors加入对列，并把这个节点标记
   为检查过
3. 重复第二步，直到对列的所有节点都检查过了，返回False

通过描述我们可以看到，BFS需要检查图中每一个节点，如果这个节点不是我们要找的节点，那么还需要把它的所有neighbors 加入队列，所以还要检查所有的边，因此BFS的时间复杂度为O(V + E)，V for vertices，E for edges。

描述完算法，我们可以实例化一个场景，并用Go语言实现。这里我们借用图书Grokking Algorithms的例子 -- Find The Mango Seller。

BTW：其实这几篇关于算法的post都是自己读Grokking Algorithms的一些笔记，这是一本非常棒的算法入门书，而且我会向身边任何对算法感兴趣的新手推荐这本书。

例子是这样的，现在你有一批芒果需要出售，要在自己的Facebook朋友圈中找到一个mango seller，把自己的芒果出售给他。

假设你的朋友圈是这样的：

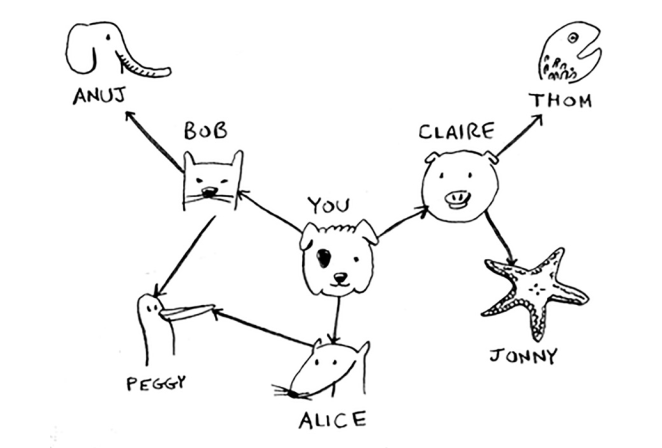
mango seller graph

那么你应该怎么做呢？

用BFS就可以很好的解决这个问题，我们从“You”出发，把“You”的三个朋友加入对列。然后从对列中取出一个朋友，判断他是不是mango seller。如果是，那么我们返回True；反之，把他标记为已搜索，并把他的朋友也加入列队。接着，重复这一过程，直到图中的所有节点都检查过，返回False。这里多嘴一句，怎样把朋友标记为“已经搜索” 呢？这是一个查重问题，而我们知道一种数据结构专门可以解决查重问题，也许你已经想起来了，那就是Hash Table！

这里是go语言的实现。

以上。