Greedy Algorithm
今天我们来介绍一下贪心算法(Greedy Algorithm)。贪心算法的基本思想是,解决问题的每一步都追求 最优,那么得到的最终结果就是最优的结果。
咋一听起来,感觉有些极端,而且很容易就可以举出一个反例来说明贪心算法不适用的情况, 比如我们上一篇讲到的背包问题。 按照贪心算法的思路,我们4lbs的背包容量,只能装下一个STEREO,总价值也就是$3000,与我们使用 动态规划得到的最优解$4500相比差了不少。但是贪心算法有它自己的适用范围,尤其是对解决NP完全问题(NP-Complete) 有着很重要的意义。
我们先来介绍一下NP完全问题。NP完全问题是指一个没有快速解法的问题,唯一的方法就是列出问题的所有可能发生的 情况,然后从这些情况中选择一个最优解。比如我们常说的旅行家问题(Traveling Salesperson Problem)。 旅行家问题是指一个旅行家想要去5个景点,而且他想知道哪条路线旅行这5个景点路程最短。这个问题唯一的解法就是 把旅行这五个景点的每一条路线都列出来,然后从中找一个最短的路线,这个方法的时间复杂度为O(n!)。显然,这个时间复 杂度并不怎么好。
对于NP完全问题,贪心算法可以为它提供解药,它可以以较快的方式尽可能地逼近最优方案。比如我们现在就可以提 出一个解决旅行家问题的贪心算法:从五个点中随意选一个点作为起始点。对于每一个起始点,都选择距它最近的邻居 节点做为下一个起始点,并把连接它们的边做为路线。这样做直到图中所有的点都被连接起来。看,这样的话, 解决旅行家问题的时间复杂度就变成了O(n)。相较最优解法的O(n!)有了相当大的提高。
经过上面的描述,相信你已经能感觉出来,贪心算法并不是为了给你最优的解法,而是作为一种估计(Approximation)算法 存在。当你遇到一个问题,解决这个问题消耗的时间非常大,最优解法的性价比非常低的时候,比如上面提到的NP完全问题, 这时,贪心算法就可以派上用场。
衡量贪心算法有这么两个因素:
- 它运行的到底比最优解法快多少
- 它与最优解的差距有多大
在了解完贪心算法的思想,应用场景和衡量因素之后,我们再来看一个贪心算法解决NP完全问题例子。
假设有一组广播电台,数量为n,每个电台可以覆盖美国几个特定的城市:
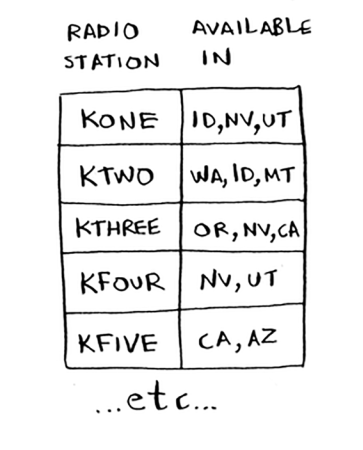
每个电台覆盖的城市可能有重复。现在问如何从这些电台中选取一组电台,在可以覆盖美国所有城市的情况下 让选取电台的数量最小?
首先这是一个NP完全问题。我们先看常规的解法:
- 求出这n个电台的所有子集
- 从中找到一个子集,使得既可以覆盖美国的所有城市,同时数量最少
这样的解法需要求出n个电台的所有子集的个数为2^n,所以时间复杂度为O(2^n)。这样的花销是十分恐怖的。 所以我们退而求其次,选择贪心算法求解,思路如下:
- 我们每次都从这n个电台中选择可以覆盖最多当前未覆盖的城市的电台,即使和之前选择的电台有重复 覆盖的城市也没有关系
- 重复第一步,直到所有的美国城市都被覆盖
最后,是Go语言的实现:
package main
import (
"fmt"
)
type States []string
type Stations map[string]States
func (s *States) Substract(t States) {
for _, str := range t {
for i := range *s {
if (*s)[i] == str {
copy((*s)[i:], (*s)[i+1:])
*s = (*s)[:len(*s)-1]
break
}
}
}
}
func (s *States) Intersection(t States) States {
ret := States{}
for _, str := range t {
for i := range *s {
if (*s)[i] == str {
ret = append(ret, str)
}
}
}
return ret
}
var (
statesNeeded States
currentStations Stations
finalStations Stations
)
func init() {
statesNeeded = States{"mt", "wa", "or", "id", "nv", "ut", "ca", "az"}
currentStations = Stations{
"kone": States{"id", "nv", "ut"},
"ktwo": States{"wa", "id", "mt"},
"kthree": States{"or", "nv", "ca"},
"kfour": States{"nv", "ut"},
"kfive": States{"ca", "az"},
}
finalStations = Stations{}
}
func getResultGreedily() {
for len(statesNeeded) > 0 {
bestStation := ""
bestStationCoveredStates := States{}
for station, states := range currentStations {
if _, ok := finalStations[station]; ok {
continue
}
covered := states.Intersection(statesNeeded)
if len(covered) > len(bestStationCoveredStates) {
bestStation = station
bestStationCoveredStates = covered
}
}
finalStations[bestStation] = bestStationCoveredStates
statesNeeded.Substract(bestStationCoveredStates)
}
}
func main() {
getResultGreedily()
fmt.Println(finalStations)
}
以上。