这篇文章我们举两个例子，看看为什么我认为Dijkstra's Algorithm可以适用于有回路图（Cyclic Graph）， 但是不适用于带负权图（Negative Weighted Graph）。

上一篇的算法如下：

   --> 当有节点可以处理
  |            |
  |            V
  |    找出这些节点中距start节点最近的节点
  |            |
  |            V
  |    更新这些节点的邻居节点
  |            |
  |            V
  |    如果有邻居节点被更新了，则更新它的parent
  |            |
  |            V
  |    标记这个节点已经被处理过了
  |            |
   ------------

我们先来看有回路图，如下面这张图：

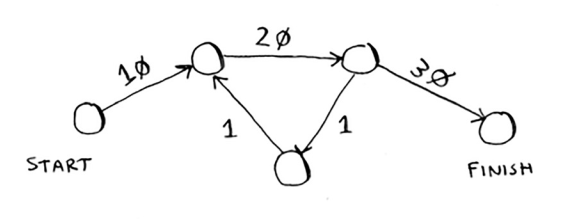
图非常简单，而且我们很容易就可以得出从start到finish的最短花销为60。 如果按照上述算法计算从start到finish的最短路径的话，我们得出的也是60，和期待的并无分别。 所以，图中有无回路对Dijkstra's Algorithm没有影响。

我们再来看负权图，如下面这张图：

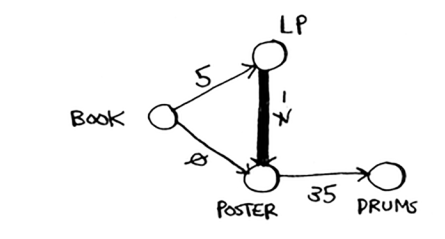
其中LP节点到到POSTER节点的权值是-7，我们知道如果沿着BOOK -> LP -> POSTER -> PRUMS是 由BOOK到PRUMS的最短路径，花销为33。但是，Dijkstra's Algorithm并不这么想。我们来跟着 算法走一遍。

先找一个BOOK能到达的最近的节点，到LP的花销为5，到POSTER的花销为0，到PRUMS的花销为无穷， 所以我们选POSTER。然后我们来更新POSTER的邻居节点。我们发现POSTER只有一个邻居PRUMS， 到它的花销为35，小于之前的无穷，所以更新由BOOK到PRUMS的花销为35，PRUMS的parent为POSTER， 并把POSTER节点标记为“处理过”。接下来，BOOK能到达的最近的节点为LP节点，LP节点只有一个邻居， 就是POSTER，结果发现由BOOK通过LP到达POSTER节点的总花销为-2，小于之前的0，所以更新由BOOK 到POSTER的花销为-2，并将POSTER的parent更新为LP，并把LP节点标记为“处理过”。然后，图中没有处理过 的节点就剩花销为35的PRUMS，然而PRUMS没有邻居节点，所以程序结束。结论为从BOOK到PRUMS的 最短路径BOOK -> POSTER -> PRUMS，花销为35。

所以看到了，对于负权图Dijkstra's Algorithm得到了一个明显错误的结果，因此Dijkstra's Algorithm 并不适用于负权图。事实上，对于负权图的最短路径问题有一个专门的算法来进行求解 -- Bellman-Ford Algorithm。感兴趣的同学可以了解一下，这里就不做介绍了。

以上。