Dijkstra's Algorithm
上一篇 介绍了广度优先搜索,一种可以对有向无权图搜索节点的图算法。今天我们来介绍一种 对有向有权图的求最短路径的算法 -- Dijkstra's Algorithm。
书中说Dijkstra's Algorithm 只适用于有向无回路图(DAG: Directed Acyclic Graph),对于图中 有回路的图和带负权的图是不适用的。注意,这里说的“不适用”是指,在这两种图中,Dijkstra's Algorithm求得的路径有可能不是最短路径。但是依我目前的理解,我觉得有回路的图 Dijkstra's Algorithm是可以处理的,而带负权图确实存在Dijkstra's Algorithm不能处理的 情况,这篇文章在本文的基础上介绍了我这样说的原因,有兴趣的小伙伴可以了解一下,这里就不多说了。
好,话不多说,我们先来看算法描述,假设我们想求一个图中节点A到节点B的最短路径,那么:
1. 找出当前节点A可以到达的最近的节点
2. 检查是否有更少的花销到达这个节点的邻居节点,
如果有,那么则更新它们的开销
3. 对图中的每个节点都进行上述两步
4. 最后得到的到节点B的开销就是A到B的最短路径
接下来,我们来举例,并用Go语言实现。
我们就拿书中的例子来讲吧,现在我们求下图中节点start到finish的最短路径:
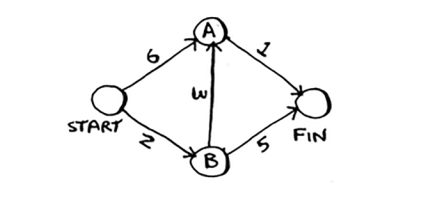
要解决这个问题,我们需要三个哈希表,它们分别是:
- 记录图中每一个节点和它的邻居节点及边的权值,类型为map[string]map[string]int
- 记录start节点到其它节点的最小花销,类型为map[string]int
- 记录从节点的parent节点,意思是start节点从parent节点到这个节点的花销最少,类型为map[string]string
我们的方法如下:
--> 当有节点可以处理
| |
| V
| 找出这些节点中距start节点最近的节点
| |
| V
| 更新这些节点的邻居节点
| |
| V
| 如果有邻居节点被更新了,则更新它的parent
| |
| V
| 标记这个节点已经被处理过了
| |
------------
最后是我们的Golang实现:
package main
import "fmt"
// define types
type Graph map[string]map[string]int
type Costs map[string]int
type Parents map[string]string
type Processed map[string]bool
// define variables
var (
graph Graph
costs Costs
parents Parents
processed Processed
)
const infinity = 10000
func init() {
graph = make(Graph)
costs = make(Costs)
parents = make(Parents)
processed = make(Processed)
graph["start"] = map[string]int{"a": 6, "b": 2}
graph["a"] = map[string]int{"finish": 1}
graph["b"] = map[string]int{"a": 3, "finish": 5}
costs["a"] = 6
costs["b"] = 2
costs["finish"] = infinity
parents["a"] = "start"
parents["b"] = "start"
parents["finish"] = ""
}
func dijkstra() {
node := findLowestCostNode()
for node != "" {
for neighbor, neighborCost := range graph[node] {
newCost := costs[node] + neighborCost
if costs[neighbor] > newCost {
costs[neighbor] = newCost
parents[neighbor] = node
}
}
processed[node] = true
node = findLowestCostNode()
}
}
func findLowestCostNode() string {
lowCostNode := ""
lowCost := infinity
for node, cost := range costs {
if cost < lowCost && !processed[node] {
lowCostNode = node
lowCost = cost
}
}
return lowCostNode
}
func printShortPath() {
node := "finish"
parentNode := parents[node]
fmt.Printf("%s", node)
for parentNode != "" {
fmt.Printf(" <- ")
node = parentNode
parentNode = parents[node]
fmt.Printf("%s", node)
}
fmt.Println()
}
func printShortCost() {
fmt.Printf("Shortest cost: %d\n", costs["finish"])
}
func main() {
dijkstra()
printShortPath()
printShortCost()
}
以上。